R
Roman aus Wien
- Registriert
- 26.03.2006
- Beiträge
- 101
- Reaktionen
- 3
Weil immer wieder Fragen nach den Schwingungsfrequenzen der Töne kommen, habe ich hier die grundlegenden Zusammenhänge zwischen den Noten (Tonhöhen) und ihren Schwingungsfrequenzen (bei der gleichstufigen bzw. gleichschwebenden Stimmung) zusammengestellt.
Im Allgemeinen nehmen wir Menschen Reizänderungen relativ und nicht absolut wahr (Weber-Fechnersches Gesetz). Es besteht also zwischen der Reizstärke (Tonhöhe, Lautstärke, Lichtstärke, Druck, usw.) und der Empfindungsstärke ein logarithmischer Zusammenhang. Wir hören, sehen und fühlen also zumeist logarithmisch. Das hat den großen Vorteil, dass wir wesentlich größere Spannweiten von Reizstärken wahrnehmen können als dies bei einem linearen Reizstärke-Empfindungsstärke-Verhältnis der Fall wäre.
Tonabstände werden dann als gleich groß empfunden, wenn sie das selbe Frequenz-Verhältnis bzw. die selbe relative Frequenzänderung haben. Die Oktave ist vom ersten Oberton abgeleitet. Jeder Oktavabstand bedeutet eine Verdoppelung der Tonfrequenz. Die Frequenzen aller von einem Ton ausgehenden Oktaven bilden somit eine geometrische Folge mit dem Faktor 2 [1, 2, 4, 8, 16, …]. Jede Oktave ist in 12 Halbtonschritte unterteilt. Die Frequenzen der Halbtöne bilden ebenfalls eine geometrische Folge. Die Tonfrequenz erhöht sich bei jedem Halbtonschritt mit dem selben Faktor, der sich einfach ermitteln lässt:
Bei 12 Halbtonschritten innerhalb einer Oktave wird dieser Faktor zwölfmal mit sich selbst multipliziert. Die zwölfte Potenz des Faktors muss also 2 ergeben. Das Frequenzverhältnis zwischen den Halbtönen ist somit die zwölfte Wurzel aus zwei (12√2 = 1,0595). Mit anderen Worten: Die Tonfrequenz steigt bei jedem Halbtonschritt um 5,95 %.
Ausgehend von einem Ton mit bekannter Tonfrequenz können die Frequenzen aller anderen Töne leicht berechnet werden:
f2 = f1•2^(n/12)
f2 ....... gesuchte Tonfrequenz
f1 ....... bekannte Tonfrequenz
n ....... Halbtonschritte zwischen Ton1 und Ton2
wenn Ton2 höher als Ton1: n > 0 (1, 2, 3, 4, 5, ….)
wenn Ton2 tiefer als Ton1: n < 0 (-1, -2, -3, -4, …)
Da heutzutage mit Taschenrechnern und Tabellenkalkulationsprogrammen Potenzen einfach berechnet werden können, verzichte ich hier darauf, die obige Formel zu logarithmieren - wie das früher notwendig war, um die Potenz in ein Produkt umzuwandeln. Wer noch das Glück hatte, in der Schule mit dem Rechenschieber zu rechnen, schafft das Logarithmieren der Gleichung ohnehin selber.
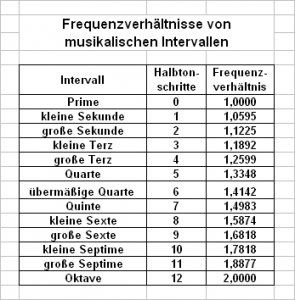
Für diejenigen, die lieber in einer Tabelle nachschauen, als selber zu rechnen, habe ich solche Tabellen als Bilder beigefügt.
Wer es genauer wissen und noch mehr erfahren will, dem empfehle ich den Abschnitt „akkustische Grundlagen der Musik“ von Jörg Gedan (http://www.pian-e-forte.de/texte/index.htm)
Roman aus Wien
Im Allgemeinen nehmen wir Menschen Reizänderungen relativ und nicht absolut wahr (Weber-Fechnersches Gesetz). Es besteht also zwischen der Reizstärke (Tonhöhe, Lautstärke, Lichtstärke, Druck, usw.) und der Empfindungsstärke ein logarithmischer Zusammenhang. Wir hören, sehen und fühlen also zumeist logarithmisch. Das hat den großen Vorteil, dass wir wesentlich größere Spannweiten von Reizstärken wahrnehmen können als dies bei einem linearen Reizstärke-Empfindungsstärke-Verhältnis der Fall wäre.
Tonabstände werden dann als gleich groß empfunden, wenn sie das selbe Frequenz-Verhältnis bzw. die selbe relative Frequenzänderung haben. Die Oktave ist vom ersten Oberton abgeleitet. Jeder Oktavabstand bedeutet eine Verdoppelung der Tonfrequenz. Die Frequenzen aller von einem Ton ausgehenden Oktaven bilden somit eine geometrische Folge mit dem Faktor 2 [1, 2, 4, 8, 16, …]. Jede Oktave ist in 12 Halbtonschritte unterteilt. Die Frequenzen der Halbtöne bilden ebenfalls eine geometrische Folge. Die Tonfrequenz erhöht sich bei jedem Halbtonschritt mit dem selben Faktor, der sich einfach ermitteln lässt:
Bei 12 Halbtonschritten innerhalb einer Oktave wird dieser Faktor zwölfmal mit sich selbst multipliziert. Die zwölfte Potenz des Faktors muss also 2 ergeben. Das Frequenzverhältnis zwischen den Halbtönen ist somit die zwölfte Wurzel aus zwei (12√2 = 1,0595). Mit anderen Worten: Die Tonfrequenz steigt bei jedem Halbtonschritt um 5,95 %.
Ausgehend von einem Ton mit bekannter Tonfrequenz können die Frequenzen aller anderen Töne leicht berechnet werden:
f2 = f1•2^(n/12)
f2 ....... gesuchte Tonfrequenz
f1 ....... bekannte Tonfrequenz
n ....... Halbtonschritte zwischen Ton1 und Ton2
wenn Ton2 höher als Ton1: n > 0 (1, 2, 3, 4, 5, ….)
wenn Ton2 tiefer als Ton1: n < 0 (-1, -2, -3, -4, …)
Da heutzutage mit Taschenrechnern und Tabellenkalkulationsprogrammen Potenzen einfach berechnet werden können, verzichte ich hier darauf, die obige Formel zu logarithmieren - wie das früher notwendig war, um die Potenz in ein Produkt umzuwandeln. Wer noch das Glück hatte, in der Schule mit dem Rechenschieber zu rechnen, schafft das Logarithmieren der Gleichung ohnehin selber.
Für diejenigen, die lieber in einer Tabelle nachschauen, als selber zu rechnen, habe ich solche Tabellen als Bilder beigefügt.
Wer es genauer wissen und noch mehr erfahren will, dem empfehle ich den Abschnitt „akkustische Grundlagen der Musik“ von Jörg Gedan (http://www.pian-e-forte.de/texte/index.htm)
Roman aus Wien