- Registriert
- 17.06.2013
- Beiträge
- 14.565
- Reaktionen
- 27.425
Folge dem Video um zu sehen, wie unsere Website als Web-App auf dem Startbildschirm installiert werden kann.
Anmerkung: Diese Funktion ist in einigen Browsern möglicherweise nicht verfügbar.


Ja! Wie hast du es gelöst?Passen ca. 21,9%?
Kommt darauf an, was Du unter dieser Summe verstehst.
Grüße
Häretiker
PS:
https://4gravitons.wordpress.com/20...natural-numbers-zeta-function-regularization/
Ist das dann bei dem Toast nicht ein Quadrat mit der halben Kantenlänge?Nein, leider falsch. Bitte auch Lösungsidee beschreiben!
Es geht auch ohne trigonometrische Funktionen. Ich habs so gelöst:
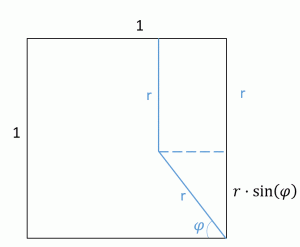
Der Einfachkeit halber nehmen wir an dass das Brot begrenzt wird durch |x|<1, |y|<1.
Der Teil der gegessen wird sind also die Punkte so dass sqrt(x^2+y^2) < min (1-|x|, 1-|y|).
Da das ganze symmetrisch ist reicht es wenn wir uns den oberen Quadranten anschauen, also 0<|x|<y. Die Gleichung vereinfacht sich dadurch zu
sqrt(x^2 + y^2) < 1-y
Aufgelöst nach x ergibt dies:
y< -x^2/2 + 1/2
also eine Parabel.
Die Endpunkte liegen auf der Linie |x|=y., also (sqrt2-1,sqrt2-1) und (1-sqrt2,sqrt2-1).
Jetzt können wir durch Integration die Fläche zwischen der Parabel und der X-Achse finden.
Wenn wir die Funktion oben von 1-sqrt2 bis sqrt2-1 integrieren, erhalten wir 2/3 * (2-sqrt2).
Davon müssen wir noch die Fläche der beiden Dreiecke mit Breite und Höhe sqrt2-1 abziehen.
Damit ergibt sich die Lösung (4*sqrt2-5)/3, oder etwa 21,9%.
Ich verstehe zwar auch nur Bahnhof aber die Frage in Verbindung mit der Skizze von Raffaello lässt für mich nur einen logischen Schluss zu: die Quadratur des Kreises. Endlich weiß ich, was damit gemeint ist.und jetzt bitte noch so formulieren, dass es auch ein Nicht-Mathe Dozent versteht

[...]
zumal die Krustenbreite ja variiert
 LG, -Rev.-
LG, -Rev.-zumal die Krustenbreite ja variiert
Zwar hat Mathematik in weiten Teilen mit operationalisierter Logik zu tun, aber fürs "logische Denken" braucht es begriffliche Inhalte, die man nur begrenzt auf Formeln reduzieren kann.
Im Mathematikunterricht in der Schule ist man vor allem damit konfrontiert, Dinge hinzunehmen und diese hingenommenen Dinge möglichst ohne störende Nebengedanken anzuwenden.
dass er von einem Butterbrot nur die Teile isst, die näher am Zentrum dran sind als am Rand.
Das Butterbrot ist exakt quadratisch. Welchen Anteil (in Prozent) des Butterbrots wird er essen?
 Ich habe schon beim Einschulungstest den stellvertretenden Schulleiter darauf hingewiesen, dass die Aufgabenstellung nicht eindeutig und die Aufgabe somit nicht zu lösen ist, falls er sie nicht zu präzisieren gewillt ist. Das hat mich damals so irritiert, dass ich mich bis heute an die Szene erinnern kann.
Ich habe schon beim Einschulungstest den stellvertretenden Schulleiter darauf hingewiesen, dass die Aufgabenstellung nicht eindeutig und die Aufgabe somit nicht zu lösen ist, falls er sie nicht zu präzisieren gewillt ist. Das hat mich damals so irritiert, dass ich mich bis heute an die Szene erinnern kann.Bei diesem Beispiel würde ich mich vor allem daran stören, dass der Butterbrot sich durch den Aufstrich von Butter verdichtet. Je nach Konsistenz des Teigs und Streichfähigkeit der Butter verzerrt es sich. Ich bin also gezwungen, diese für mich realistischen Nebengedanken willkürlich herunterzuschlucken und sturheil die passende Formel anzuwenden, obwohl ich weiß, dass das Ergebnis der Realität nicht entspricht.
Eigentlich sind es zwei wichtige Kompetenzen, die der Mathematikunterricht vermitteln sollte. Neben dem reinen logischen Denken, die Fähigkeit, sinnvoll zu abstrahieren.
Die Alternative wäre halt, einfach nur die symbolische Aufgabe zu stellen: "Gegeben sei ein Quadrat. Berechnen Sie den Anteil der Punkte, die näher am Mittelpunkt als am Rand des Quadrats sind".
Mathematik hat erstmal nichts mit der Realität zu tun
Und das ist eben kein (strikt) logisches Denken.
 Man gaukelt eine Realität vor, die keine ist - oder umgekehrt, man fordert die Lerngruppe auf, sämtliche Realitätserfahrungen willkürlich auszublenden, die das angestrebte "idealisierte" Ergebnis normalerweise ("logischerweise") mit beeinflussen würden. Die abstrakte Formulierung wie von @Klaus dargestellt, wäre ehrlich und der Sache angemessen, denn es geht gar nicht um Realität, sondern um Abstracta, die ohne Einflussfaktoren axiomatisch gesetzt sind.
Man gaukelt eine Realität vor, die keine ist - oder umgekehrt, man fordert die Lerngruppe auf, sämtliche Realitätserfahrungen willkürlich auszublenden, die das angestrebte "idealisierte" Ergebnis normalerweise ("logischerweise") mit beeinflussen würden. Die abstrakte Formulierung wie von @Klaus dargestellt, wäre ehrlich und der Sache angemessen, denn es geht gar nicht um Realität, sondern um Abstracta, die ohne Einflussfaktoren axiomatisch gesetzt sind.Und es wäre toll, wenn das auch mal explizit im Matheunterricht erwähnt werden würde. Um den Leuten klar zu machen: Wenn ihr irgendwie quantitive Aussagen über die Welt gewinnen wollt, braucht ihr mehr oder weniger beide Aspekte.
Kaum eine Wissemschaft kommt gänzlich ohne aus.

. Ich lerne also, das Denken tunlichst bleiben zu lassen und die richtige Formel anzuwenden.
Kleines Beispiel: Den aktuellen Konflikt zwischen Madrid und Barcelona kann ich Dir folgerichtig aus der Heiratspolitik einer bestimmten Familie ab dem 15. Jh. ableiten.

